Arrow's Impossibility Theorem

Arrow's Impossibility Theorem, a fundamental concept in social choice theory, has been a cornerstone of understanding the challenges inherent in aggregating individual preferences to form a collective decision. This theorem, first introduced by Kenneth Arrow in 1951, asserts that no voting system can perfectly satisfy a set of reasonable criteria when making decisions, particularly in the context of more than two options. The implications of Arrow's theorem are far-reaching, influencing fields from economics and political science to philosophy and computer science. At its core, the theorem highlights the intrinsic difficulties in designing a fair, democratic system that accurately reflects the will of the people.
Introduction to Arrow’s Impossibility Theorem

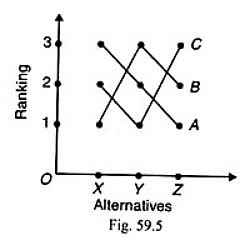
The theorem is based on several key criteria that any fair voting system should meet: non-dictatorship (no single voter should have the power to impose their preference on the group), universal domain (the system should be able to handle any set of individual preferences), independence of irrelevant alternatives (the introduction or removal of an alternative should not affect the relative ranking of other alternatives), and the Pareto principle (if all individuals prefer one option over another, the group preference should reflect this). Additionally, the system should be transitive, meaning if option A is preferred to option B, and option B is preferred to option C, then option A should be preferred to option C. Arrow’s theorem shows that it is impossible for any voting system to satisfy all these conditions simultaneously in all possible worlds, especially when there are more than two alternatives.
Key Components and Implications
A critical component of Arrow’s theorem is the concept of a “social welfare function,” which is a rule for transforming individual preferences into a collective preference. The theorem essentially states that there cannot exist a social welfare function that satisfies all the specified conditions for all possible profiles of individual preferences. This has profound implications for democratic theory and practice, suggesting that no electoral system can be perfectly fair or representative. For instance, in a world where citizens have diverse and potentially conflicting preferences, any system designed to aggregate these preferences into a collective choice will inherently have flaws, whether it be susceptibility to strategic voting, the inability to handle certain types of preferences, or a failure to ensure that the outcome reflects the true will of the majority.
| Condition | Description |
|---|---|
| Non-dictatorship | No single voter has complete control over the outcome. |
| Universal Domain | The system can handle any possible set of individual preferences. |
| Independence of Irrelevant Alternatives | The introduction or removal of an alternative does not affect the ranking of other alternatives. |
| Pareto Principle | If all individuals prefer A to B, then A should be preferred to B in the collective ranking. |
| Transitivity | The collective preference is logically consistent, meaning if A is preferred to B, and B is preferred to C, then A is preferred to C. |

Practical Applications and Limitations
Despite the pessimistic tone of Arrow’s theorem, it has inspired a rich field of research into voting systems and social choice theory. Many approaches have been developed to address the limitations outlined by the theorem, including efforts to design voting systems that, while not perfect, can minimize certain types of flaws or biases. For example, systems like ranked-choice voting or the Borda count have been proposed as alternatives to traditional plurality voting, each with its strengths and weaknesses. The key is to understand the trade-offs involved with each system and to select one that best fits the specific context in which it will be used.
Evaluating Voting Systems
Evaluating the efficacy of different voting systems involves a nuanced understanding of the criteria outlined in Arrow’s theorem, as well as empirical analysis of how these systems perform in real-world scenarios. This includes examining the susceptibility of a system to strategic voting, its ability to handle diverse preference profiles, and its overall fairness and representativeness. Furthermore, considerations such as simplicity, transparency, and the potential for voter confusion must also be taken into account, as these factors can significantly influence the effectiveness and acceptance of a voting system.
Key Points
- Arrow's Impossibility Theorem highlights the challenges in aggregating individual preferences into a collective decision.
- No voting system can perfectly satisfy criteria like non-dictatorship, universal domain, independence of irrelevant alternatives, the Pareto principle, and transitivity.
- The theorem has significant implications for democratic theory and practice, suggesting inherent flaws in any electoral system.
- Understanding and addressing these challenges is crucial for effective decision-making and ensuring the collective choice reflects individual preferences as closely as possible.
- Practical applications involve designing voting systems that minimize flaws, considering trade-offs, and selecting systems that fit specific contexts.
As social choice theory continues to evolve, the insights provided by Arrow's Impossibility Theorem remain foundational. By recognizing the inherent limitations of collective decision-making processes, we can strive to create systems that, while imperfect, better serve the needs and preferences of all individuals involved. This pursuit of better, more representative democratic processes is ongoing, influenced by Arrow's seminal work and the profound implications it has for how we understand and approach collective decision-making.
What are the main implications of Arrow’s Impossibility Theorem for democratic systems?
+The theorem implies that no democratic system can perfectly aggregate individual preferences into a collective decision without violating at least one reasonable condition such as non-dictatorship, universal domain, independence of irrelevant alternatives, or the Pareto principle.
How does Arrow’s theorem influence the design of voting systems?
+The theorem encourages the development of voting systems that, while not perfect, minimize certain types of flaws or biases. It prompts a careful consideration of the trade-offs involved in designing a system that balances fairness, representativeness, and simplicity.
What are some potential alternatives to traditional voting systems suggested by research following Arrow’s theorem?
+Alternatives include ranked-choice voting, the Borda count, and other systems designed to reduce the impact of certain biases or flaws identified by Arrow’s theorem. Each has its strengths and weaknesses, and the choice of system depends on the specific context and goals of the decision-making process.