Derivative Of Pi

The derivative of pi, often denoted as π, is a concept that has garnered significant attention in mathematical circles. Pi, being a constant approximately equal to 3.14159, represents the ratio of a circle's circumference to its diameter. In mathematics, the derivative of a function or a constant is a measure of how that function or constant changes as its input changes. However, when dealing with constants like pi, the derivative is straightforward: the derivative of a constant is always zero.
This is because the derivative of a constant function, by definition, does not change. A constant function, including one that represents the value of pi, does not vary with respect to any variable. For instance, if we consider the function f(x) = π, regardless of the value of x, f(x) remains constant at π. The rate of change of a constant with respect to any variable is zero, which is why the derivative of pi (or any other constant) with respect to any variable is 0.
Key Points
- The derivative of a constant, including pi, is always zero because constants do not change with respect to any variable.
- Pi, being a constant, does not have a changing value, hence its derivative is 0.
- In calculus, the derivative of a function represents the rate of change of the function with respect to one of its variables.
- For any constant function f(x) = c, where c is a constant (like pi), the derivative f'(x) is 0.
- The concept of the derivative of pi might seem trivial, but it underscores the fundamental principles of calculus and the nature of constants in mathematical functions.
Calculus and Constants
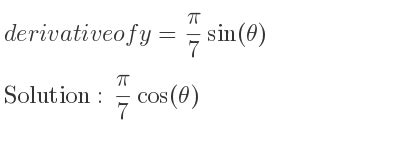
In the realm of calculus, understanding the behavior of functions and their rates of change is crucial. Constants like pi play a significant role in various mathematical formulas and equations, especially in geometry and trigonometry. The fact that the derivative of pi is zero reflects the static nature of constants within dynamic mathematical frameworks. This concept is essential for solving problems that involve differentiation, where identifying constants and their derivatives as zero simplifies the calculation process.
Derivative Rules
There are several rules in calculus that help in finding the derivatives of functions, including the power rule, product rule, quotient rule, and chain rule. However, when these rules are applied to constant functions, the outcome is always the same: a derivative of zero. This is because the derivative measures the rate of change, and since constants do not change, there is no rate of change to measure.
| Function Type | Derivative |
|---|---|
| Constant (e.g., f(x) = π) | 0 |
| Linear (e.g., f(x) = 2x + π) | 2 |
| Polynomial (e.g., f(x) = x^2 + πx) | Depends on the polynomial (e.g., 2x + π for the given example) |

Applications and Implications

The fact that the derivative of pi is zero has practical implications in various fields, including physics and engineering. For instance, in the study of circular motion, the constant π appears in equations describing the relationship between the radius of a circle and its circumference or area. When differentiating these equations to find rates of change (like the speed of an object moving in a circular path), the derivative of pi as zero simplifies the calculations, reflecting the unchanging nature of π in these contexts.
Moreover, understanding that constants have a derivative of zero is crucial for optimizing functions in calculus, especially in problems involving maxima and minima. It helps in identifying which parts of a function contribute to its rate of change and which do not, thereby streamlining the optimization process.
Mathematical Evolution
The concept of pi and its derivative reflects the evolutionary nature of mathematics. From ancient civilizations’ approximations of pi to modern calculus, the understanding of mathematical constants and their properties has deepened. The recognition that the derivative of pi is zero is a testament to the development of calculus as a tool for analyzing change and rates of change in mathematical functions.
Furthermore, the study of pi's properties and its appearances in various mathematical formulas has led to a greater understanding of geometry, algebra, and analysis. This, in turn, has facilitated advancements in science and technology, underscoring the interconnectedness of mathematical concepts and their practical applications.
What is the derivative of a constant in calculus?
+The derivative of a constant in calculus is always zero. This is because constants, by definition, do not change with respect to any variable, hence their rate of change is zero.
Is pi considered a constant in mathematics?
+Yes, pi (π) is considered a constant in mathematics. It represents the ratio of a circle's circumference to its diameter and is approximately equal to 3.14159. As a constant, its derivative is zero.
What are the practical implications of the derivative of pi being zero?
+The practical implications include simplifications in calculus calculations, especially in problems involving circular motion or optimization. Recognizing that the derivative of pi is zero streamlines the differentiation process and reflects the unchanging nature of pi in mathematical equations.
In conclusion, the derivative of pi being zero is a fundamental concept in calculus, reflecting the static nature of mathematical constants within dynamic frameworks. This understanding is crucial for various applications in mathematics, physics, and engineering, showcasing the significance of constants like pi in the broader context of mathematical and scientific inquiry.



