Electric Power Formula

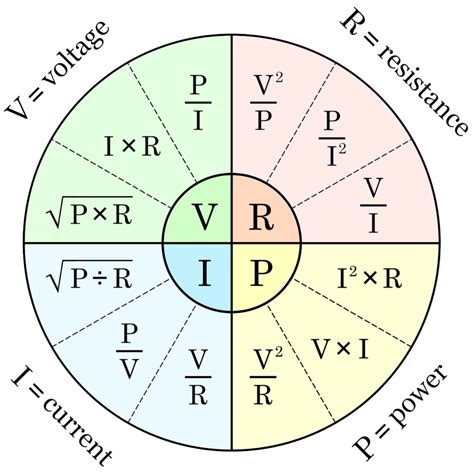
The electric power formula is a fundamental concept in the field of electrical engineering, describing the relationship between the voltage, current, and power in an electrical circuit. The formula is expressed as P = V x I, where P represents the power in watts (W), V represents the voltage in volts (V), and I represents the current in amperes (A). This formula is crucial in understanding the behavior of electrical systems, from simple household circuits to complex industrial power distribution networks.
In addition to the basic formula, there are other variations that take into account the power factor (PF) and the root mean square (RMS) values of voltage and current. For instance, in AC circuits, the power formula can be expressed as P = V x I x PF, where PF is a dimensionless quantity between 0 and 1 that represents the ratio of real power to apparent power. Understanding these formulas is essential for designing and analyzing electrical systems, ensuring they operate efficiently and safely.
Key Points
- The electric power formula is given by P = V x I, where P is the power in watts, V is the voltage in volts, and I is the current in amperes.
- The power factor (PF) is crucial in AC circuits, where the formula becomes P = V x I x PF, reflecting the efficiency of power usage.
- Understanding the electric power formula is vital for the design, analysis, and optimization of electrical systems, including both DC and AC circuits.
- Real-world applications of the electric power formula include the calculation of power consumption in household appliances, the design of electrical grids, and the efficiency analysis of industrial machinery.
- The formula also underpins the development of renewable energy systems, such as solar and wind power, where maximizing power output is critical.
Derivation and Explanation of the Electric Power Formula

The electric power formula, P = V x I, can be derived from the definition of power as the rate of doing work. In an electrical context, work is done when a charge is moved against an electric field, and the rate at which this work is done gives us the power. The voltage (V) represents the electric potential difference, or the “pressure” driving electric current through a circuit, while the current (I) represents the rate at which charge flows. Thus, the product of voltage and current gives the total power being transferred in the circuit.
Power Factor and Its Impact on Electric Power
In alternating current (AC) systems, the power factor (PF) plays a significant role. The PF is defined as the ratio of the real power (P) flowing through the circuit to the apparent power (S), which is the vector sum of real and reactive power. It can be expressed as PF = P / S = cos(θ), where θ is the phase angle between the voltage and current waveforms. A higher power factor indicates that more of the current is being used to do real work, increasing the efficiency of the system. Power factor correction techniques, such as using capacitors or inductors, are often employed to improve the PF and thus reduce the apparent power requirements of a system.
| Quantity | Unit | Description |
|---|---|---|
| Power (P) | Watt (W) | Rate of doing work |
| Voltage (V) | Volts (V) | Electric potential difference |
| Current (I) | Amperes (A) | Rate of charge flow |
| Power Factor (PF) | Unitless | Efficiency of power usage in AC circuits |
Applications of the Electric Power Formula

The electric power formula has widespread applications across various fields. In residential settings, it’s used to calculate the power consumption of appliances and the total energy bill. In industrial settings, understanding the power requirements of machinery and systems is crucial for ensuring reliable operation and minimizing downtime. The formula also underpins the design and optimization of electrical grids, including the integration of renewable energy sources and the implementation of smart grid technologies.
Efficiency and Safety Considerations
Beyond the calculation of power, the electric power formula highlights the importance of efficiency and safety in electrical systems. High-efficiency systems not only reduce energy consumption but also minimize the risk of overheating and electrical fires. Safety considerations, such as proper insulation, grounding, and circuit protection, are also critical in preventing electrical accidents. By applying the electric power formula and considering these factors, engineers and technicians can ensure that electrical systems operate safely and efficiently.
What is the difference between real power, reactive power, and apparent power in AC circuits?
+Real power (P) is the actual power used by a circuit to perform work, measured in watts (W). Reactive power (Q) is the power that flows back and forth between the source and the load without doing any work, measured in vars. Apparent power (S) is the vector sum of real and reactive power, measured in volt-amperes (VA), and represents the maximum power that can be delivered by a source.
How does the power factor affect the efficiency of an electrical system?
+A high power factor (close to 1) indicates that the current is in phase with the voltage, meaning that the real power is maximized, and the reactive power is minimized. This results in more efficient use of the electrical system, reducing energy losses and increasing the overall power factor of the system.
What are some common applications of the electric power formula in everyday life?
+The electric power formula is used in a wide range of applications, from calculating the power consumption of household appliances to designing electrical grids and optimizing industrial machinery. It's also essential for the development of renewable energy systems, such as solar and wind power, where maximizing power output is critical.
In conclusion, the electric power formula is a fundamental principle that underlies the functioning of electrical systems. By understanding and applying this formula, individuals can gain insights into the behavior of electrical circuits, optimize system performance, and contribute to the development of more efficient and sustainable electrical technologies. As the world continues to rely on electrical energy for an increasing range of applications, the importance of the electric power formula will only continue to grow.



