How Many Sides Does A Polygon Have To Have
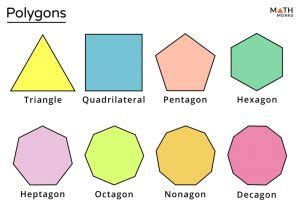
A polygon, by definition, is a two-dimensional shape with at least three sides. The term "polygon" comes from the Greek words "poly" meaning many and "gon" meaning angle. The number of sides a polygon has can vary greatly, and each type of polygon with a specific number of sides has its own name.
Types of Polygons Based on the Number of Sides

The simplest polygon is a triangle, which has three sides. Following the triangle, as we increase the number of sides, we get quadrilaterals (four sides), pentagons (five sides), hexagons (six sides), heptagons (seven sides), octagons (eight sides), and so on. The naming convention for polygons follows a pattern where the prefix indicates the number of sides (e.g., mono- for one, di- for two, tri- for three, etc.), and the suffix “-gon” denotes the shape as a polygon.
Polygon Properties and Characteristics
Each type of polygon has its unique properties and characteristics. For instance, a regular polygon, where all sides and angles are equal, exhibits symmetry. The internal angles of a polygon, which are the angles inside the shape, add up to a specific total that can be calculated using the formula (n-2) * 180 degrees, where n is the number of sides. This formula applies to all polygons, regardless of the number of sides they have.
| Number of Sides | Polygon Name | Internal Angles Sum |
|---|---|---|
| 3 | Triangle | 180 degrees |
| 4 | Quadrilateral | 360 degrees |
| 5 | Pentagon | 540 degrees |
| 6 | Hexagon | 720 degrees |
| n | n-gon | (n-2) * 180 degrees |
Mathematical Exploration of Polygons

Mathematicians have extensively studied polygons, exploring their geometric properties, such as perimeter, area, and the relationships between their sides and angles. The study of polygons is not only theoretically interesting but also has practical applications in various fields, including architecture, engineering, and design. For example, understanding the properties of regular polygons is crucial for designing structures that are aesthetically pleasing and structurally sound.
Real-World Applications of Polygons
Polygons are all around us, from the tiles on our bathroom floors to the walls of our homes. The choice of polygon in design can affect the appearance, durability, and functionality of a structure. For instance, hexagonal tiles are often used in flooring because they can cover a surface with minimal gaps, making them efficient and visually appealing. Similarly, in nature, the hexagonal shape of honeycombs provides maximum storage space while using the least amount of wax, showcasing the efficiency of polygonal structures in biological systems as well.
Key Points
- A polygon must have at least three sides to be considered a polygon.
- The naming of polygons is based on the number of sides, with specific prefixes and the suffix "-gon".
- The internal angles of a polygon add up to (n-2) * 180 degrees, where n is the number of sides.
- Regular polygons have all sides and angles equal, exhibiting symmetry.
- Polygons have practical applications in architecture, engineering, design, and are observed in natural patterns.
In conclusion, the number of sides a polygon can have is theoretically unlimited, but each specific number of sides gives the polygon unique properties and applications. Understanding these properties not only enhances our knowledge of geometry but also informs us about the intricate patterns and structures found in both natural and man-made environments.
What is the minimum number of sides a polygon can have?
+A polygon must have at least three sides to be considered a polygon. A shape with fewer than three sides does not enclose an area and thus does not meet the definition of a polygon.
How are polygons named based on their number of sides?
+Polygons are named using a prefix that indicates the number of sides and the suffix “-gon”. For example, a triangle (three sides) and a hexagon (six sides) follow this naming convention.
What is the formula for the sum of internal angles of a polygon?
+The sum of the internal angles of a polygon can be calculated using the formula (n-2) * 180 degrees, where n is the number of sides of the polygon.