L Associated Graphs
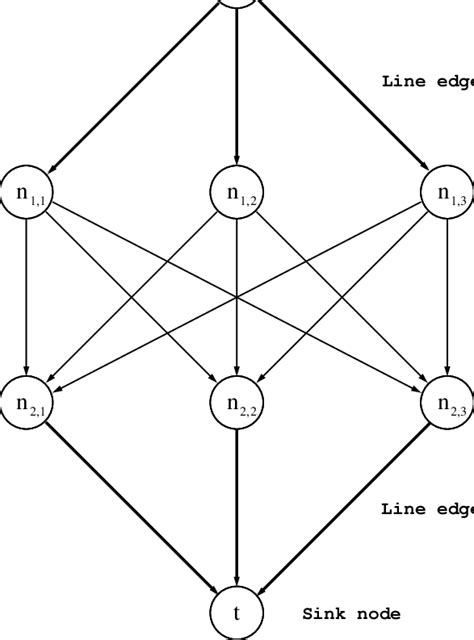
Associated graphs play a crucial role in understanding and visualizing complex data in various fields, including mathematics, physics, computer science, and engineering. These graphs are used to represent relationships between objects, and their associated properties, allowing for a deeper understanding of the underlying structures and patterns. In this article, we will delve into the world of associated graphs, exploring their definitions, types, applications, and importance in different domains.
Definition and Types of Associated Graphs

Associated graphs are mathematical constructs that represent relationships between objects, such as nodes or vertices, and their associated properties, like edges or links. These graphs can be categorized into different types, including:
- Undirected Graphs: These graphs have edges that do not have a direction, representing a two-way relationship between nodes.
- Directed Graphs: These graphs have edges with a direction, representing a one-way relationship between nodes.
- Weighted Graphs: These graphs have edges with weights or labels, representing the strength or cost of the relationship between nodes.
- Unweighted Graphs: These graphs have edges without weights or labels, representing a simple relationship between nodes.
Applications of Associated Graphs
Associated graphs have numerous applications in various fields, including:
| Field | Application |
|---|---|
| Computer Science | Network topology, data structures, algorithm design |
| Physics | Particle interactions, quantum mechanics, network analysis |
| Engineering | Network design, optimization, control systems |
| Mathematics | Graph theory, combinatorics, algebra |

Importance of Associated Graphs
Associated graphs are essential in understanding and analyzing complex systems and networks, as they provide a visual representation of relationships and interactions between objects. The importance of associated graphs can be seen in their ability to:
- Model Complex Systems: Associated graphs can represent complex systems, such as social networks, transportation networks, and biological systems, allowing for a deeper understanding of their behavior and dynamics.
- Analyze Network Properties: Associated graphs enable the analysis of network properties, such as connectivity, centrality, and community structure, which are crucial in understanding network behavior and optimizing network performance.
- Optimize Network Performance: Associated graphs can be used to optimize network performance, such as minimizing latency, maximizing throughput, and reducing energy consumption, which is essential in designing efficient networks.
Key Points
- Associated graphs represent relationships between objects and their associated properties.
- There are different types of associated graphs, including undirected, directed, weighted, and unweighted graphs.
- Associated graphs have numerous applications in computer science, physics, engineering, and mathematics.
- The study of associated graphs has led to numerous breakthroughs in understanding complex systems and networks.
- Associated graphs are essential in modeling complex systems, analyzing network properties, and optimizing network performance.
In conclusion, associated graphs are a fundamental concept in understanding complex systems and networks, and their applications are diverse and widespread. By studying associated graphs, researchers and practitioners can gain valuable insights into the behavior and dynamics of complex systems, enabling the development of more efficient algorithms, protocols, and models.
What are associated graphs used for?
+Associated graphs are used to represent relationships between objects and their associated properties, and have numerous applications in computer science, physics, engineering, and mathematics.
What are the different types of associated graphs?
+There are different types of associated graphs, including undirected, directed, weighted, and unweighted graphs, each with its own unique properties and applications.
Why are associated graphs important?
+Associated graphs are essential in understanding and analyzing complex systems and networks, enabling the development of more efficient algorithms, protocols, and models, and have numerous applications in various fields.