Lateral Surface Area Of A Triangular Prism

The lateral surface area of a triangular prism is a fundamental concept in geometry, and it's essential to understand its calculation to solve various problems in mathematics and real-world applications. In this article, we will delve into the world of triangular prisms, exploring their properties, and providing a step-by-step guide on how to calculate the lateral surface area.
Understanding Triangular Prisms

A triangular prism is a three-dimensional solid object with two identical faces that are triangles. The other faces are rectangles, and the edges are the lines where the faces meet. The triangular prism has a unique property: it has a lateral surface area, which is the sum of the areas of its rectangular faces.
Key Components of a Triangular Prism
To calculate the lateral surface area of a triangular prism, we need to understand its key components. These include:
- Base triangles: The two identical triangular faces of the prism.
- Rectangular faces: The faces that connect the base triangles, also known as the lateral faces.
- Height: The distance between the two base triangles, measured perpendicular to the base.
- Base perimeter: The sum of the lengths of the sides of the base triangle.
Key Points
- The lateral surface area of a triangular prism is the sum of the areas of its rectangular faces.
- The formula for the lateral surface area is: LSA = ph, where p is the base perimeter and h is the height.
- The base perimeter is the sum of the lengths of the sides of the base triangle.
- The height of the prism is measured perpendicular to the base.
- Understanding the properties of triangular prisms is crucial for calculating their lateral surface area.
Calculating the Lateral Surface Area
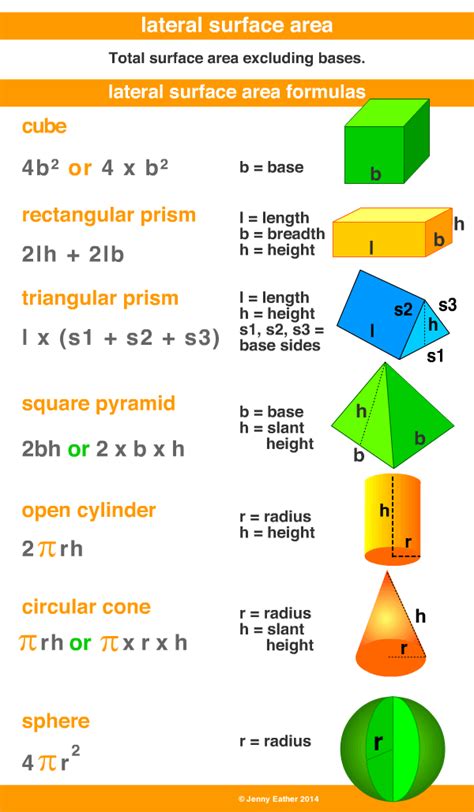
The lateral surface area of a triangular prism can be calculated using the formula: LSA = ph, where p is the base perimeter and h is the height. To calculate the base perimeter, we need to find the lengths of the sides of the base triangle and add them together.
Step-by-Step Calculation
Here’s a step-by-step guide to calculate the lateral surface area of a triangular prism:
- Find the lengths of the sides of the base triangle.
- Calculate the base perimeter by adding the lengths of the sides together.
- Measure the height of the prism, which is the distance between the two base triangles.
- Multiply the base perimeter by the height to get the lateral surface area.
| Component | Formula | Description |
|---|---|---|
| Base Perimeter | p = a + b + c | The sum of the lengths of the sides of the base triangle. |
| Height | h | The distance between the two base triangles, measured perpendicular to the base. |
| Lateral Surface Area | LSA = ph | The sum of the areas of the rectangular faces. |

Real-World Applications
The lateral surface area of a triangular prism has numerous real-world applications. For instance, in architecture, the lateral surface area of a building can affect its energy efficiency and structural integrity. In engineering, the lateral surface area of a component can impact its stress resistance and durability.
Practical Examples
Here are some practical examples of how the lateral surface area of a triangular prism is used in real-world applications:
- Building design: Architects use the lateral surface area of a building to determine its energy efficiency and structural integrity.
- Component design: Engineers use the lateral surface area of a component to determine its stress resistance and durability.
- Packaging design: The lateral surface area of a package can affect its stability and shipping costs.
What is the formula for the lateral surface area of a triangular prism?
+The formula for the lateral surface area of a triangular prism is: LSA = ph, where p is the base perimeter and h is the height.
How do I calculate the base perimeter of a triangular prism?
+To calculate the base perimeter, find the lengths of the sides of the base triangle and add them together: p = a + b + c.
What are some real-world applications of the lateral surface area of a triangular prism?
+The lateral surface area of a triangular prism has numerous real-world applications, including building design, component design, and packaging design.
In conclusion, the lateral surface area of a triangular prism is a fundamental concept in geometry, and its calculation is crucial for various real-world applications. By understanding the properties of triangular prisms and following the step-by-step guide, you can accurately calculate the lateral surface area and apply it to solve problems in mathematics and real-world scenarios.



