Rational Irrational Numbers

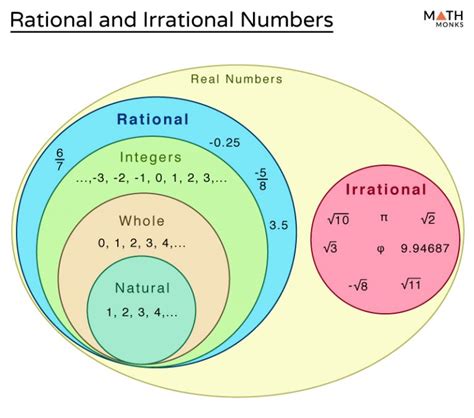
The realm of numbers is a vast and intricate tapestry, woven from threads of rational and irrational numbers. At its core, the distinction between these two categories lies in their ability to be expressed as simple fractions. Rational numbers, such as 1/2 or 3/4, can be represented as the quotient of two integers, with the denominator being non-zero. On the other hand, irrational numbers, like π (pi) or the square root of 2, cannot be expressed in this manner, as their decimal expansions are infinite and non-repeating.
The concept of irrational numbers has its roots in ancient Greece, where mathematicians such as Pythagoras and Euclid grappled with the nature of reality and the fundamental principles of mathematics. The discovery of irrational numbers is often attributed to the Pythagorean school, who encountered them while attempting to calculate the length of the diagonal of a square. This led to a profound crisis in the understanding of mathematics, as it challenged the long-held belief that all numbers could be expressed as simple ratios of integers.
Key Points
- Rational numbers can be expressed as simple fractions, whereas irrational numbers cannot.
- Irrational numbers have infinite and non-repeating decimal expansions.
- The discovery of irrational numbers dates back to ancient Greece, where mathematicians like Pythagoras and Euclid explored their properties.
- The existence of irrational numbers led to a significant shift in the understanding of mathematics, challenging the notion that all numbers could be expressed as simple ratios.
- Irrational numbers play a crucial role in various mathematical concepts, including geometry, trigonometry, and calculus.
Nature of Irrational Numbers

Irrational numbers are often characterized by their unique properties, which set them apart from rational numbers. One of the most distinctive features of irrational numbers is their ability to be expressed as infinite, non-repeating decimal expansions. For example, the decimal representation of π is 3.14159265358979323846…, with no discernible pattern or repetition. This property has significant implications for mathematical operations, as it affects the way irrational numbers are added, subtracted, multiplied, and divided.
Examples of Irrational Numbers
Some notable examples of irrational numbers include the square root of 2 (√2), the square root of 3 (√3), and the golden ratio (φ). These numbers have been extensively studied and have numerous applications in mathematics, science, and engineering. The square root of 2, for instance, is an essential component in the construction of the Pythagorean theorem, while the golden ratio appears in various aspects of geometry, art, and design.
| Mathematical Constant | Approximate Value |
|---|---|
| π (pi) | 3.14159265358979323846... |
| √2 (square root of 2) | 1.41421356237309504880... |
| √3 (square root of 3) | 1.73205080756887729352... |
| φ (golden ratio) | 1.61803398874989502654... |
Role of Irrational Numbers in Mathematics

Irrational numbers play a vital role in various mathematical concepts and theories. In geometry, irrational numbers are used to describe the lengths and proportions of shapes, such as the diagonal of a square or the ratio of the circumference of a circle to its diameter. In trigonometry, irrational numbers appear in the form of sine, cosine, and tangent values for certain angles. Furthermore, irrational numbers are essential in calculus, where they are used to define limits, derivatives, and integrals.
Applications of Irrational Numbers
The applications of irrational numbers are diverse and widespread, ranging from science and engineering to art and design. In physics, irrational numbers are used to describe the behavior of waves, particles, and forces. In engineering, irrational numbers are employed in the design of bridges, buildings, and electronic circuits. In art and design, irrational numbers appear in the form of geometric patterns, fractals, and self-similar shapes.
In conclusion, irrational numbers are a fundamental component of mathematics, with unique properties and far-reaching implications. Their discovery in ancient Greece led to a significant shift in the understanding of mathematics, and their study has continued to evolve over the centuries. As mathematics continues to advance, the role of irrational numbers will remain essential, providing a foundation for developing new concepts, models, and theories that describe the world around us.
What is the difference between rational and irrational numbers?
+Rational numbers can be expressed as simple fractions, whereas irrational numbers cannot be expressed in this manner and have infinite, non-repeating decimal expansions.
What are some examples of irrational numbers?
+Examples of irrational numbers include π (pi), the square root of 2 (√2), the square root of 3 (√3), and the golden ratio (φ).
What is the role of irrational numbers in mathematics?
+Irrational numbers play a vital role in various mathematical concepts, including geometry, trigonometry, and calculus, and are essential for developing advanced mathematical models and theories.
