Rectangular To Polar
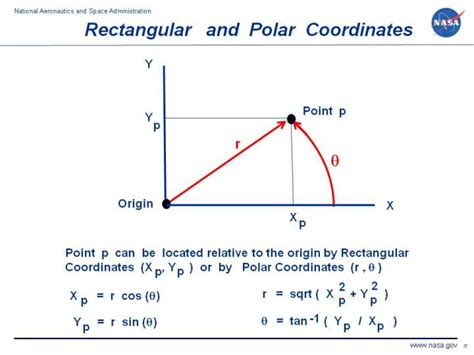
The conversion from rectangular to polar coordinates is a fundamental concept in mathematics and engineering, particularly in fields such as signal processing, control systems, and electrical engineering. This conversion process involves transforming coordinates from the Cartesian (rectangular) plane to the polar plane, where each point is represented by its distance from the origin (radius) and the angle formed with the positive x-axis (azimuth). Understanding the principles behind this conversion is crucial for various applications, including filtering, modulation, and navigation systems.
Key Points
- The rectangular to polar conversion involves calculating the magnitude (radius) and angle (azimuth) of a vector given its x and y components.
- The formula for calculating the magnitude is r = \sqrt{x^2 + y^2}, and for the angle, \theta = \tan^{-1}\left(\frac{y}{x}\right).
- Understanding the quadrant in which the point lies is crucial for determining the correct angle, as the arctan function returns values between -\frac{\pi}{2} and \frac{\pi}{2}.
- Polar coordinates offer a convenient representation for periodic signals and systems, facilitating operations such as multiplication and division, which correspond to rotation and scaling in the polar domain.
- Applications of rectangular to polar conversion include signal processing, navigation, and the analysis of complex systems where rotational symmetry is present.
Mathematical Foundation

The mathematical foundation for converting rectangular coordinates ((x, y)) to polar coordinates ((r, \theta)) is based on trigonometry. The relationship between the two systems can be described by the following equations: (x = r \cos(\theta)) and (y = r \sin(\theta)). To convert from rectangular to polar, we use the inverse relationships: (r = \sqrt{x^2 + y^2}) for the radius, and (\theta = \tan^{-1}\left(\frac{y}{x}\right)) for the angle. It is essential to consider the quadrant of the point ((x, y)) to ensure the angle (\theta) is correctly determined, as the arctan function returns values within the range of (-\frac{\pi}{2}) to (\frac{\pi}{2}).
Quadrant Consideration
Determining the correct quadrant for the angle (\theta) is vital because the arctan function does not provide information about the quadrant. The quadrant can be identified based on the signs of (x) and (y): if (x > 0) and (y > 0), the point is in the first quadrant; if (x < 0) and (y > 0), it is in the second quadrant; if (x < 0) and (y < 0), it is in the third quadrant; and if (x > 0) and (y < 0), it is in the fourth quadrant. Adjustments to (\theta) may be necessary based on the quadrant: for points in the second quadrant, (\theta = \pi + \tan^{-1}\left(\frac{y}{x}\right)); for the third quadrant, (\theta = \pi + \tan^{-1}\left(\frac{y}{x}\right)); and for the fourth quadrant, (\theta = 2\pi + \tan^{-1}\left(\frac{y}{x}\right)), considering the periodic nature of angles.
| Quadrant | x | y | Adjustment to \theta |
|---|---|---|---|
| I | + | + | \theta = \tan^{-1}\left(\frac{y}{x}\right) |
| II | - | + | \theta = \pi + \tan^{-1}\left(\frac{y}{x}\right) |
| III | - | - | \theta = \pi + \tan^{-1}\left(\frac{y}{x}\right) |
| IV | + | - | \theta = 2\pi + \tan^{-1}\left(\frac{y}{x}\right) |
Practical Applications

The conversion from rectangular to polar coordinates has numerous practical applications across various fields. In signal processing, polar coordinates can simplify the representation of signals that have rotational symmetry or where the magnitude and phase of the signal are of interest. In navigation, particularly with the use of GPS, converting between rectangular and polar coordinates is essential for determining distances and directions between locations on the Earth’s surface. Furthermore, in electrical engineering, the analysis of AC circuits often involves the use of polar coordinates to represent impedance and admittance, facilitating the calculation of circuit parameters such as voltage, current, and power.
Signal Processing Example
In signal processing, consider a complex signal represented in rectangular coordinates as (x(t) = 3\cos(2\pi ft) + 4\sin(2\pi ft)), where (f) is the frequency of the signal. To convert this signal into polar form, we first recognize it as a sum of sine and cosine functions, which can be represented as a single sinusoidal function with a phase shift, (x(t) = A\cos(2\pi ft + \phi)), where (A = \sqrt{3^2 + 4^2} = 5) and (\phi = \tan^{-1}\left(\frac{4}{3}\right)). This conversion simplifies the analysis and manipulation of the signal, especially when considering operations like modulation and demodulation.
What is the primary benefit of converting rectangular coordinates to polar coordinates in signal processing?
+The primary benefit is the simplification of signal representation, especially for periodic signals, allowing for easier analysis and manipulation of signal properties like magnitude and phase.
How do you determine the correct quadrant for the angle \theta in polar coordinates?
+The quadrant is determined by the signs of x and y: the first quadrant if both are positive, the second if x is negative and y is positive, the third if both are negative, and the fourth if x is positive and y is negative. Adjustments to \theta are made accordingly to ensure it falls within the correct range.
What are some practical applications of rectangular to polar conversion?
+Applications include signal processing for easier manipulation of periodic signals, navigation for determining distances and directions, and electrical engineering for analyzing AC circuits and representing impedance and admittance in a more convenient form.
In conclusion, the conversion from rectangular to polar coordinates is a fundamental process with deep roots in trigonometry and broad applications across various fields. Understanding the principles behind this conversion, including the determination of the correct quadrant for the angle, is essential for effectively working with and analyzing systems that involve rotational motion or periodic phenomena. The ability to convert between these coordinate systems seamlessly opens up new avenues for simplifying complex problems and gaining insights into the behavior of signals and systems.


