Routh Hurwitz Criterion
The Routh-Hurwitz criterion is a mathematical tool used to determine the stability of a linear time-invariant system. It is a powerful method for analyzing the roots of a characteristic equation, which is essential in control systems engineering. The criterion was first introduced by Edward John Routh in 1877 and later improved by Adolf Hurwitz in 1895. In this article, we will delve into the details of the Routh-Hurwitz criterion, its significance, and its application in control systems.
Introduction to the Routh-Hurwitz Criterion

The Routh-Hurwitz criterion is based on the idea that the stability of a system can be determined by examining the roots of its characteristic equation. The characteristic equation is a polynomial equation that describes the behavior of the system. The roots of this equation represent the poles of the system, which are critical in determining its stability. The Routh-Hurwitz criterion provides a systematic approach to determining the stability of a system by examining the coefficients of the characteristic equation.
Mathematical Formulation
The Routh-Hurwitz criterion is applied to a characteristic equation of the form:
ansn + an-1sn-1 +… + a1s + a0 = 0
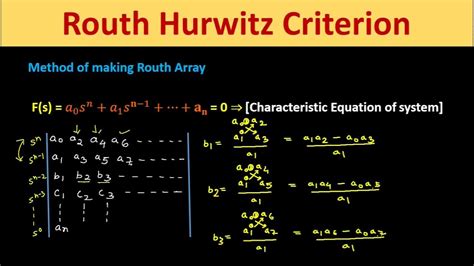
where ai are the coefficients of the polynomial, and s is the complex variable. The criterion involves constructing a table of coefficients, known as the Routh array, which is used to determine the stability of the system. The Routh array is constructed by arranging the coefficients of the characteristic equation in a specific pattern.
| Row | coefficients |
|---|---|
| 1 | an, an-2, an-4,... |
| 2 | an-1, an-3, an-5,... |
| 3 | b1, b2, b3,... |
| 4 | c1, c2, c3,... |
The elements of the Routh array are computed using the following formulas:
bi = (an-1an-2 - anan-3) / an-1
ci = (an-1b2 - b1an-3) / b1
The Routh-Hurwitz criterion states that the system is stable if and only if all the elements in the first column of the Routh array are positive.
Application of the Routh-Hurwitz Criterion

The Routh-Hurwitz criterion has numerous applications in control systems engineering. It is used to design and analyze control systems, such as feedback control systems, and to determine the stability of systems with multiple feedback loops. The criterion is also used in the design of filters, such as low-pass and high-pass filters, and in the analysis of the stability of systems with time delays.
Example Application
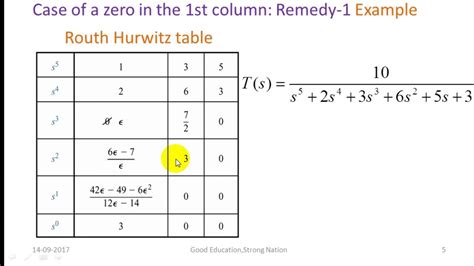
Consider a system with a characteristic equation given by:
s3 + 2s2 + 3s + 1 = 0
To determine the stability of the system, we construct the Routh array:
| Row | coefficients |
|---|---|
| 1 | 1, 3 |
| 2 | 2, 1 |
| 3 | 2.5, 0 |
Since all the elements in the first column of the Routh array are positive, the system is stable.
Key Points
- The Routh-Hurwitz criterion is a mathematical tool used to determine the stability of a linear time-invariant system.
- The criterion involves constructing a table of coefficients, known as the Routh array, which is used to determine the stability of the system.
- The Routh array is constructed by arranging the coefficients of the characteristic equation in a specific pattern.
- The elements of the Routh array are computed using specific formulas.
- The system is stable if and only if all the elements in the first column of the Routh array are positive.
Conclusion
In conclusion, the Routh-Hurwitz criterion is a powerful tool for analyzing the stability of linear time-invariant systems. It provides a systematic approach to determining the stability of a system by examining the coefficients of the characteristic equation. The criterion has numerous applications in control systems engineering and is widely used in the design and analysis of control systems.
What is the Routh-Hurwitz criterion?
+The Routh-Hurwitz criterion is a mathematical tool used to determine the stability of a linear time-invariant system.
How is the Routh array constructed?
+The Routh array is constructed by arranging the coefficients of the characteristic equation in a specific pattern.
What is the condition for stability using the Routh-Hurwitz criterion?
+The system is stable if and only if all the elements in the first column of the Routh array are positive.
Meta Description: Learn about the Routh-Hurwitz criterion, a mathematical tool used to determine the stability of linear time-invariant systems, and its applications in control systems engineering.



