Small Angle Approximation

The small angle approximation is a fundamental concept in mathematics and physics, particularly in the fields of trigonometry, calculus, and engineering. This approximation allows for the simplification of complex mathematical expressions involving trigonometric functions, making it easier to analyze and solve problems. The small angle approximation is based on the idea that for small values of an angle, the trigonometric functions can be approximated by linear functions, which are easier to work with.
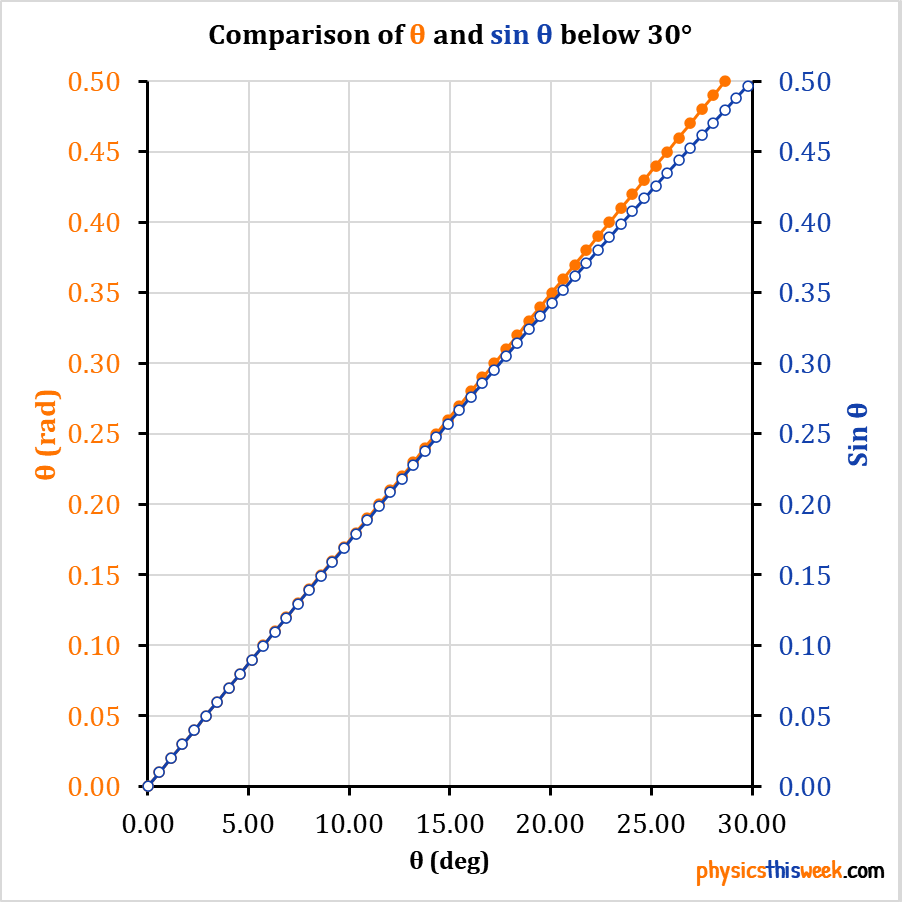
In essence, the small angle approximation states that for small angles, the sine of the angle is approximately equal to the angle itself, and the cosine of the angle is approximately equal to 1. This can be expressed mathematically as: sin(θ) ≈ θ and cos(θ) ≈ 1, where θ is the angle in radians. These approximations are valid when the angle is small, typically less than 10 degrees or 0.17 radians.
Key Points
- The small angle approximation is used to simplify complex mathematical expressions involving trigonometric functions.
- The approximation states that sin(θ) ≈ θ and cos(θ) ≈ 1 for small angles.
- The approximation is valid for angles less than 10 degrees or 0.17 radians.
- The small angle approximation is widely used in physics, engineering, and mathematics to solve problems involving oscillations, waves, and rotations.
- The approximation can be derived using the Taylor series expansion of the sine and cosine functions.
Mathematical Derivation

The small angle approximation can be derived using the Taylor series expansion of the sine and cosine functions. The Taylor series expansion of a function f(x) around a point x = a is given by: f(x) = f(a) + f’(a)(x - a) + f”(a)(x - a)^2⁄2! + f”‘(a)(x - a)^3⁄3! +…. Using this expansion, we can derive the small angle approximation for the sine and cosine functions.
For the sine function, the Taylor series expansion around x = 0 is: sin(x) = x - x^3/3! + x^5/5! - x^7/7! +.... For small values of x, the higher-order terms in the expansion can be neglected, leaving us with: sin(x) ≈ x. Similarly, for the cosine function, the Taylor series expansion around x = 0 is: cos(x) = 1 - x^2/2! + x^4/4! - x^6/6! +.... For small values of x, the higher-order terms in the expansion can be neglected, leaving us with: cos(x) ≈ 1.
Applications of the Small Angle Approximation
The small angle approximation has numerous applications in physics, engineering, and mathematics. One of the most common applications is in the study of oscillations and waves. The small angle approximation can be used to simplify the equations of motion for a pendulum, allowing for the calculation of the period and frequency of the oscillations. The approximation is also used in the study of waves, where it can be used to simplify the equations describing the propagation of waves.
In engineering, the small angle approximation is used in the design of mechanical systems, such as gears and linkages. The approximation can be used to simplify the analysis of the motion of these systems, allowing for the calculation of the forces and torques involved. The small angle approximation is also used in the field of robotics, where it can be used to simplify the analysis of the motion of robotic arms and other mechanical systems.
| Application | Description |
|---|---|
| Oscillations and Waves | The small angle approximation is used to simplify the equations of motion for a pendulum and to study the propagation of waves. |
| Engineering Design | The approximation is used to simplify the analysis of the motion of mechanical systems, such as gears and linkages. |
| Robotics | The small angle approximation is used to simplify the analysis of the motion of robotic arms and other mechanical systems. |
Limitations and Extensions

While the small angle approximation is a powerful tool, it has limitations. The approximation is only valid for small angles, and the accuracy of the approximation decreases as the angle increases. For larger angles, more sophisticated mathematical techniques, such as the use of Taylor series expansions or numerical methods, may be required to obtain accurate results.
In addition to the small angle approximation, there are other approximations that can be used to simplify mathematical expressions involving trigonometric functions. One such approximation is the large angle approximation, which is used to simplify expressions involving large angles. The large angle approximation is based on the idea that for large angles, the trigonometric functions can be approximated by exponential functions.
Another extension of the small angle approximation is the use of higher-order approximations. These approximations involve including higher-order terms in the Taylor series expansion of the trigonometric functions, allowing for more accurate results to be obtained. However, these approximations are often more complex and may require more sophisticated mathematical techniques to implement.
What is the small angle approximation?
+The small angle approximation is a mathematical technique used to simplify complex expressions involving trigonometric functions. It states that for small angles, the sine of the angle is approximately equal to the angle itself, and the cosine of the angle is approximately equal to 1.
What are the limitations of the small angle approximation?
+The small angle approximation is only valid for small angles, typically less than 10 degrees or 0.17 radians. For larger angles, more sophisticated mathematical techniques may be required to obtain accurate results.
What are some applications of the small angle approximation?
+The small angle approximation has numerous applications in physics, engineering, and mathematics, including the study of oscillations and waves, engineering design, and robotics.



