Square Root Property
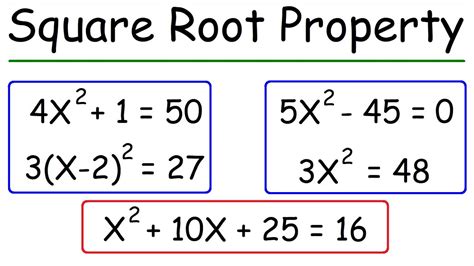
The Square Root Property is a fundamental concept in algebra, used to solve quadratic equations that can be expressed in the form of $x^2 = k$, where $k$ is a constant. This property allows us to find the solutions of such equations by taking the square root of both sides of the equation. In this article, we will delve into the details of the Square Root Property, its application, and provide examples to illustrate its usage.
Understanding the Square Root Property

The Square Root Property states that if x^2 = k, then x = \pm\sqrt{k}. This means that if we have a quadratic equation in the form of x^2 = k, we can solve for x by taking the square root of both sides of the equation. The \pm symbol indicates that there are two possible solutions, one positive and one negative, which are equal in magnitude but opposite in sign.
Application of the Square Root Property
The Square Root Property is commonly used to solve quadratic equations that can be factored or expressed in the form of x^2 = k. For example, consider the equation x^2 = 16. Using the Square Root Property, we can take the square root of both sides of the equation to get x = \pm\sqrt{16}. Simplifying further, we get x = \pm4. This means that the solutions to the equation are x = 4 and x = -4.
| Equation | Solutions |
|---|---|
| $x^2 = 16$ | $x = \pm4$ |
| $x^2 = 25$ | $x = \pm5$ |
| $x^2 = 36$ | $x = \pm6$ |

Key Considerations and Examples

When applying the Square Root Property, it’s crucial to consider the sign of the constant term k. If k is positive, the solutions will be real numbers, as we’ve seen in the previous examples. However, if k is negative, the solutions will be complex numbers. For instance, consider the equation x^2 = -16. Using the Square Root Property, we get x = \pm\sqrt{-16}. Since the square root of a negative number is not a real number, we can express the solutions as x = \pm4i, where i is the imaginary unit.
Complex Solutions and the Square Root Property
When dealing with complex solutions, it’s essential to remember that the Square Root Property still applies, but the solutions will be expressed in terms of complex numbers. For example, consider the equation x^2 = -25. Using the Square Root Property, we get x = \pm\sqrt{-25}. Simplifying further, we get x = \pm5i. This means that the solutions to the equation are x = 5i and x = -5i.
Key Points
- The Square Root Property states that if $x^2 = k$, then $x = \pm\sqrt{k}$.
- The property is used to solve quadratic equations in the form of $x^2 = k$.
- The solutions can be real or complex numbers, depending on the sign of the constant term $k$.
- When $k$ is positive, the solutions are real numbers.
- When $k$ is negative, the solutions are complex numbers.
Conclusion and Future Directions
In conclusion, the Square Root Property is a powerful tool for solving quadratic equations in the form of x^2 = k. By understanding the property and its application, we can easily solve equations and find the solutions. As we continue to explore the world of algebra, it’s essential to remember the Square Root Property and its role in solving quadratic equations. With practice and experience, we can become proficient in applying the property to solve a wide range of equations and problems.
What is the Square Root Property?
+The Square Root Property states that if x^2 = k, then x = \pm\sqrt{k}. This property is used to solve quadratic equations in the form of x^2 = k.
How do I apply the Square Root Property?
+To apply the Square Root Property, simply take the square root of both sides of the equation x^2 = k. This will give you the solutions x = \pm\sqrt{k}.
What are the solutions to the equation x^2 = 16?
+The solutions to the equation x^2 = 16 are x = 4 and x = -4.



