Vector Minus Vector
The operation of subtracting one vector from another is a fundamental concept in vector mathematics, crucial for understanding various physical and geometric phenomena. Vector subtraction, often denoted as vector minus vector, is used in a wide range of applications, from physics and engineering to computer graphics and navigation. This operation allows us to find the difference between two vectors, which can represent forces, velocities, displacements, or any other quantity with both magnitude and direction.
Understanding Vector Subtraction
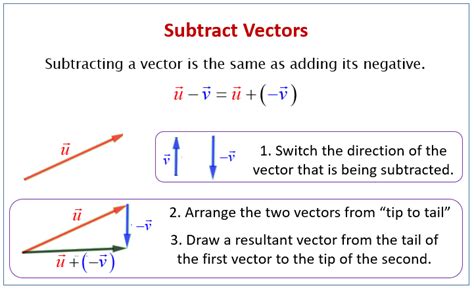
Vector subtraction is conceptually similar to vector addition but involves finding the difference between two vectors rather than their sum. Given two vectors, A and B, the subtraction of B from A (A - B) can be performed by adding A to the negative of B (A + (-B)). This process essentially involves changing the direction of vector B by reversing its arrowhead and then proceeding with vector addition. The resulting vector gives us the difference between the original vectors A and B.
Mathematical Representation
The mathematical representation of vector subtraction can be illustrated as follows: If we have two vectors A = (a1, a2, a3) and B = (b1, b2, b3), then the subtraction of B from A is given by A - B = (a1 - b1, a2 - b2, a3 - b3). This formula shows that each component of the resulting vector is the difference between the corresponding components of the original vectors.
| Vector Component | Vector A | Vector B | A - B |
|---|---|---|---|
| X-axis | a1 | b1 | a1 - b1 |
| Y-axis | a2 | b2 | a2 - b2 |
| Z-axis | a3 | b3 | a3 - b3 |
Geometric Interpretation
The geometric interpretation of vector subtraction can be visualized using the triangle law of vector addition. By constructing a triangle where vectors A and -B form two sides, the third side represents the result of A - B. This method provides a straightforward way to understand and visualize the outcome of subtracting one vector from another, helping in solving problems that involve vector differences.
Applications of Vector Subtraction
Vector subtraction has numerous applications across various fields. In physics, it is used to calculate the relative velocity between two objects moving in different directions. In computer graphics, vector subtraction is essential for calculating the position of objects in 3D space relative to each other. In engineering, it is used to determine the forces acting on structures and the stress they undergo due to external loads.
Key Points
- Vector subtraction (A - B) is equivalent to adding A to the negative of B (A + (-B)).
- The mathematical formula for subtracting vector B from vector A in three dimensions is (a1 - b1, a2 - b2, a3 - b3).
- Vector subtraction has practical applications in physics, engineering, computer graphics, and navigation.
- The geometric interpretation involves constructing a triangle where vectors A and -B are two sides, and the resulting vector is the third side.
- Mastering vector subtraction is essential for solving complex problems involving forces, velocities, and displacements in various fields.
Vector subtraction is a fundamental operation that allows us to find the difference between two vectors, which is crucial for understanding and analyzing various phenomena in physics, engineering, and other fields. By grasping the concept of vector subtraction, both mathematically and geometrically, professionals can better approach and solve complex problems that involve vector operations.
What is the difference between vector addition and vector subtraction?
+Vector addition involves combining two vectors to find their sum, while vector subtraction involves finding the difference between two vectors. Vector subtraction can be performed by adding one vector to the negative of the other vector.
How is vector subtraction used in real-world applications?
+Vector subtraction is used in various real-world applications, including calculating relative velocities in physics, determining positions in 3D graphics, and analyzing forces and stresses in engineering. It’s essential for solving problems that involve the difference between two vectors.
Can vector subtraction be performed geometrically?
+Yes, vector subtraction can be visualized and performed geometrically using the triangle law of vector addition. By constructing a triangle with vectors A and -B as two sides, the resulting vector (A - B) is represented by the third side of the triangle.



