Z Vs T Test
The Z test and the T test are two of the most commonly used statistical tests in hypothesis testing. While they share some similarities, they are used in different situations and have distinct characteristics. In this article, we will delve into the world of Z tests and T tests, exploring their definitions, applications, and key differences.
Key Points
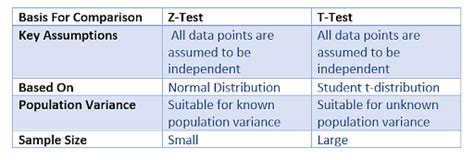
- The Z test is used when the population standard deviation is known, and the sample size is large (n ≥ 30).
- The T test is used when the population standard deviation is unknown, and the sample size is small (n < 30).
- Both tests are used to determine if there is a significant difference between the sample mean and the population mean.
- The Z test is more sensitive than the T test, but it requires more information about the population.
- The T test is more robust than the Z test, but it is less sensitive.
What is a Z Test?
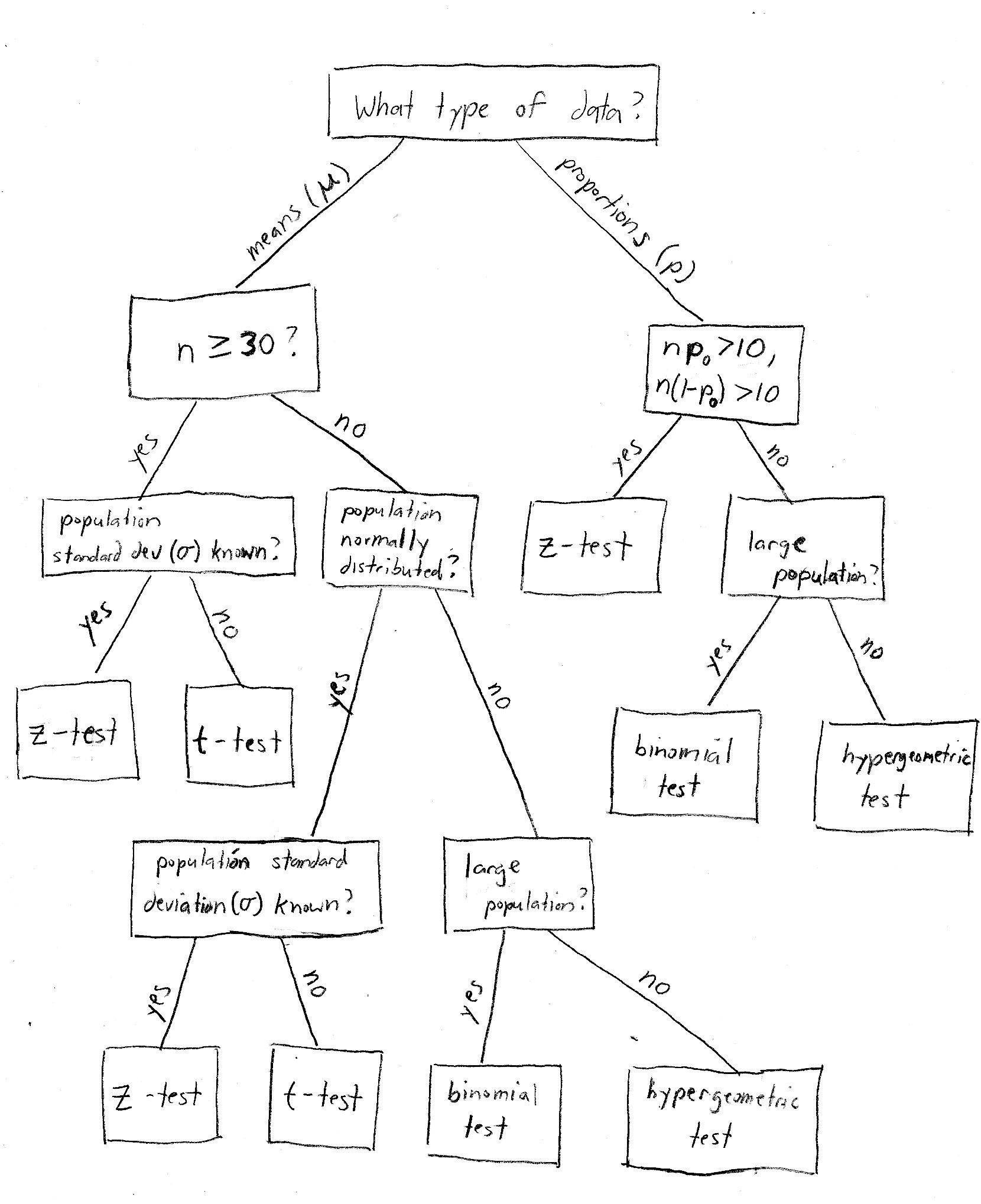
A Z test is a statistical test used to determine if there is a significant difference between the sample mean and the population mean. It is used when the population standard deviation is known, and the sample size is large (n ≥ 30). The Z test is also known as the large sample test or the normal test. The test statistic is calculated using the formula: Z = (x̄ - μ) / (σ / √n), where x̄ is the sample mean, μ is the population mean, σ is the population standard deviation, and n is the sample size.
Assumptions of the Z Test
The Z test assumes that the population is normally distributed, and the sample is randomly selected from the population. It also assumes that the population standard deviation is known, and the sample size is large. If these assumptions are not met, the Z test may not be reliable.
What is a T Test?

A T test is a statistical test used to determine if there is a significant difference between the sample mean and the population mean. It is used when the population standard deviation is unknown, and the sample size is small (n < 30). The T test is also known as the small sample test or the student’s t-test. The test statistic is calculated using the formula: t = (x̄ - μ) / (s / √n), where x̄ is the sample mean, μ is the population mean, s is the sample standard deviation, and n is the sample size.
Assumptions of the T Test
The T test assumes that the population is normally distributed, and the sample is randomly selected from the population. It also assumes that the sample size is small, and the population standard deviation is unknown. If these assumptions are not met, the T test may not be reliable.
| Test | Population Standard Deviation | Sample Size |
|---|---|---|
| Z Test | Known | Large (n ≥ 30) |
| T Test | Unknown | Small (n < 30) |

Key Differences between Z Test and T Test
The Z test and the T test have several key differences. The Z test is more sensitive than the T test, but it requires more information about the population. The T test is more robust than the Z test, but it is less sensitive. The Z test is used when the population standard deviation is known, and the sample size is large, while the T test is used when the population standard deviation is unknown, and the sample size is small.
Choosing between Z Test and T Test
When choosing between a Z test and a T test, it’s essential to consider the research question, the sample size, and the availability of information about the population standard deviation. If the research question requires a more sensitive test, and the population standard deviation is known, the Z test is the better choice. However, if the research question requires a more robust test, and the population standard deviation is unknown, the T test is more suitable.
What is the main difference between a Z test and a T test?
+The main difference between a Z test and a T test is the population standard deviation. The Z test is used when the population standard deviation is known, while the T test is used when the population standard deviation is unknown.
When should I use a Z test?
+You should use a Z test when the population standard deviation is known, and the sample size is large (n ≥ 30).
When should I use a T test?
+You should use a T test when the population standard deviation is unknown, and the sample size is small (n < 30).
Meta Description: Learn about the differences between Z tests and T tests, including when to use each and how to calculate the test statistics. Understand the assumptions and limitations of each test to make informed decisions in your research. (150 characters)